Bandwidth and Signal Analysis

Introduction:
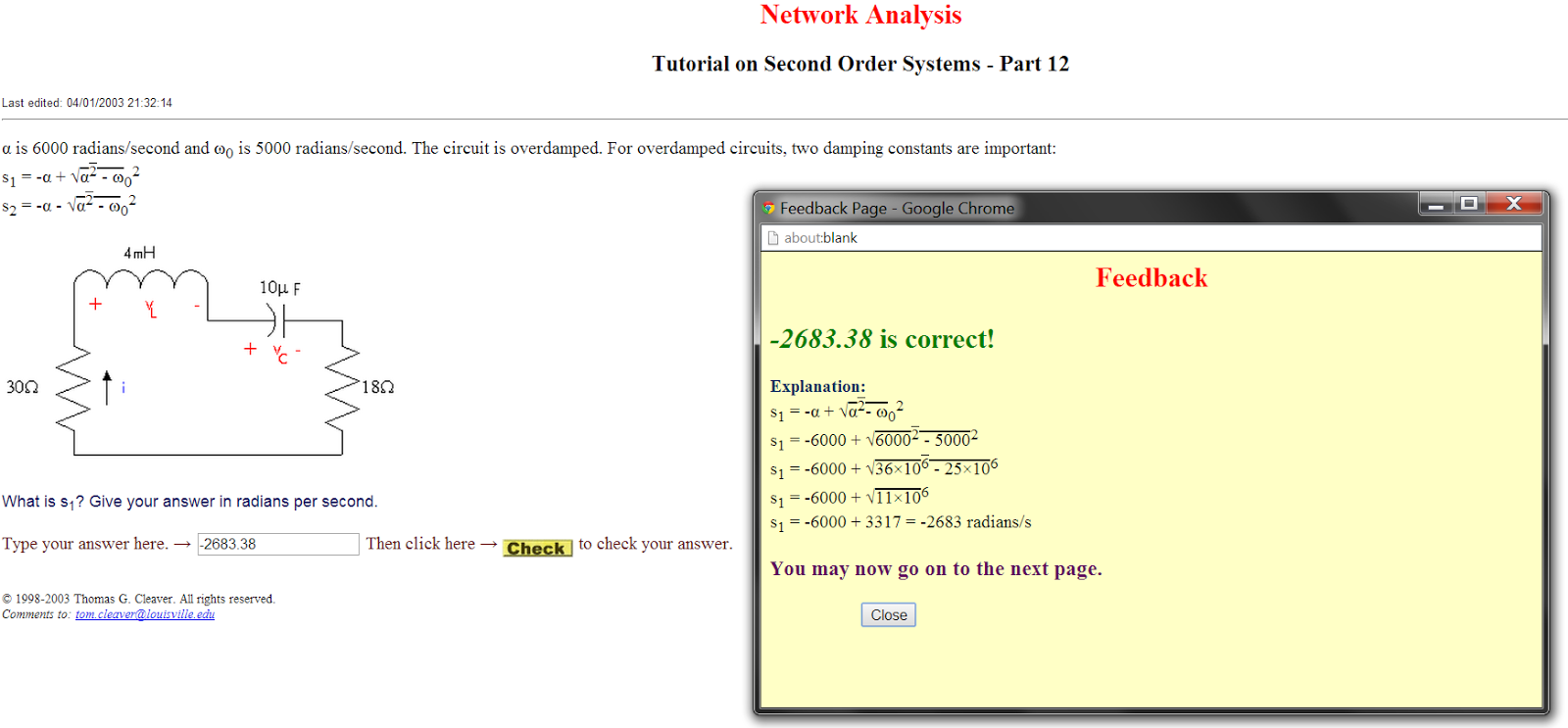
Power in an AC RLC circuit can be maximized if there is no power lost in the capacitor and inductor. This is achieved at a particular frequency known as the resonant frequency. For our purposes we can limit the frequency to a theoretical bandwidth.

Our circuit contained in:
10 Ohm and 100 Ohm resistor
1 uF and 100 uF capacitor
2.2 mH capacitor
Vmax=4.0V

To find the resonant frequency we first calculated the theoretical value for each case.

Measuring the maximum current in the circuit gave us the maximum power since Pmax=kVI
CASE 1

CASE 2

The bandwidth of the each circuit allowed us range to find the maximum current. According to the experiment the power was maximized at 34.1 mA and 148.7 mA at frequencies of 503 Hz and 5436 Hz. This disagrees with the theoretical calculation so no conclusion about resonant frequency can be reached except that resonant frequency is inversely proportional to capacitance.

Frequency Response and Filters

Objective:
A filter can be used to separate frequencies in a circuit. Two ways to do so is to use a high pass or low pass filter by adding a capacitor. We are able to test and show a filter in use by measuring the gain and voltage of a circuit with a capacitor.

First we set up a circuit for a high pass filter then a low pass filter according to the following diagrams.

This is what the circuit looked like set up

From measuring the voltage across the capacitor and resistor for a low high pass and low pass filter respectively, here are the results.

The graphs were created using a logarithmic scale and the gain can be seen as a function on the graph.

Conclusion:

Matching the theoretical gain of a high pass filter to our actual gain shows a close agreement which validates the theory of frequency filters.

AC Circuit Analysis

Complex Numbers Freemat

In this activity we learned how to use Freemat to easily calculate complex solutions.

Integrating and Differentiating Op Amps

We observed the effects of integrating and differentiating op amps

 

This integrating op amp shows the yellow sinusoidal output with smaller amplitude to the integration effect of the op amp.

At this point the op amp was becoming saturated.

This differentiating op amp created a phase shift and decrease in amplitude in yellow.

In each case the frequency was maintained despite the operations, which is expected of  AC circuits.

Network Analysis on Second Order Circuits

Capacitor Charging/Discharging

Introduction:
Capacitors are electrical components that store energy in the electric field and can rapidly charge or discharge the energy if needed. In this lab we observed the charging and discharging of a capacitor in the circuit as is dumps it energy.

Procedure:
First, we found the values of the components when the circuit is charged and discharged in the circuits below.

We used this oscilloscope to perform the lab but unfortunately it only gave instantaneous voltage. So we illustrated the response of the capacitor charging and discharging.

 We used a stopwatch and a voltmeter to measure the voltage of the charging capacitor within 20 seconds.

Materials 1 Voltmeter and 1 stopwatch (optional), 1 oscilloscope, 2 variable resistors, 1 33 microfarad capacitor, cables.

For a charging time of about 20 seconds the voltage was 11 volts. The discharge time was about 2 sectonds.

Leakage Resistance:

Error calculation:

This was how the discharging graph should have appeared over time.

Conclusion:
The lab demonstrated the rapid discharge rate of a capacitor and the reasonable energy storage that can be achieved with the correct circuitry. The experiment was valid and the leakage resistance was about 10 times the charging resistance. This was the same ratio of the charging to discharging times of the capacitor.

Practical Signal Conditioning

Introduction:

The purpose of this lab was to use an operational amplifier to perform an operation and observe a signal. We used a LM35 semiconductor to translate the ambient air temperature into a voltage signal. This would give us a temperature which would be converted into the Fahrenheit scale from the Celsius scale through the op amp. 

Procedure:
   We tested the LM35 with 9 V into it relative to ground and seeing what voltage we get as output. We go an output current of 220 mA which was a magnitude representation of the ambient room temperature.

Add caption

 We found the necessary and available resistors to get the proper conversion factors to convert the signal voltage into the comparable Fahrenheit voltage. 

We then connected the LM35 to the op amp into the circuit shown. We also used a potentiometer to adjust the input voltage and the output we got:

Using the temperature equation we found the output current to be 0716 A.

The error is shown here.

Conclusion:

This application of op amps demonstrates a practical use of signal conditioning for observing the temperature. It is much more convenient to have a real time temperature with simple signals than to have to convert the temperatures otherwise. The error may have be due to approximations in calculations.

Operational Amplifiers 1

Introduction:
The purpose of this lab is to condition a signal from a voltage input to a required voltage output.
- Set up voltage divider circuit in order to obtain signal voltage in DC
- Set up Inverting op amp circuit that conditions signal from 0 to 1 v to 0 to -10v
- measure the values
- conclusion

Procedure:
We first had to find the necessary resistors for this circuit by finding an appropriate ratio and looking at the available resistors.
-The sensor may only output a maximum of 1 mA of current.

Vcc = 12 V.
Vee = -12 V. 
Vin = 0 V to +1 V.
Vout = 0 V to -10 V.

Then we created a voltage dividing circuit that would give us the correct 1 V drop across the input and output, which can be modified with the POT.

Ry = 909 Ohm

To make sure the resistor Rx does not surpass the power limit we calculated the minimum possible resistance.

Rx_min=1152 Ohms, but we will use 1300 ohms as We used a 1300 Ohm resistor to be safe.

For Rx at 1300 Ohms we recalculated 
Ry = 118 Ohms












To avoid unappreciable loading of the divider circuit with too low resistances we used a 10k Ohm Rx value instead.

These values are what we used for our model.













By decreasing the value of the POT to a value lower than 909, we were able to obtain necessary voltages for the signal input.

This is what our circuit and testing looked like.

Testing for all the voltages and caluclating the necessary values gave us the following table.

Conclusion:

     The results conclude that there was a gain of -10 through the OP amp, which conditioned the signal to the desired voltage. The current did not exceed 1 milliamp and the voltage divider resistor remained in tact. We were able to successfully condition a signal for the various voltages and see the expected gains.