Wednesday, April 30, 2014
Monday, April 28, 2014
Capacitor Charging/Discharging
Introduction:
Capacitors are electrical components that store energy in the electric field and can rapidly charge or discharge the energy if needed. In this lab we observed the charging and discharging of a capacitor in the circuit as is dumps it energy.
Procedure:
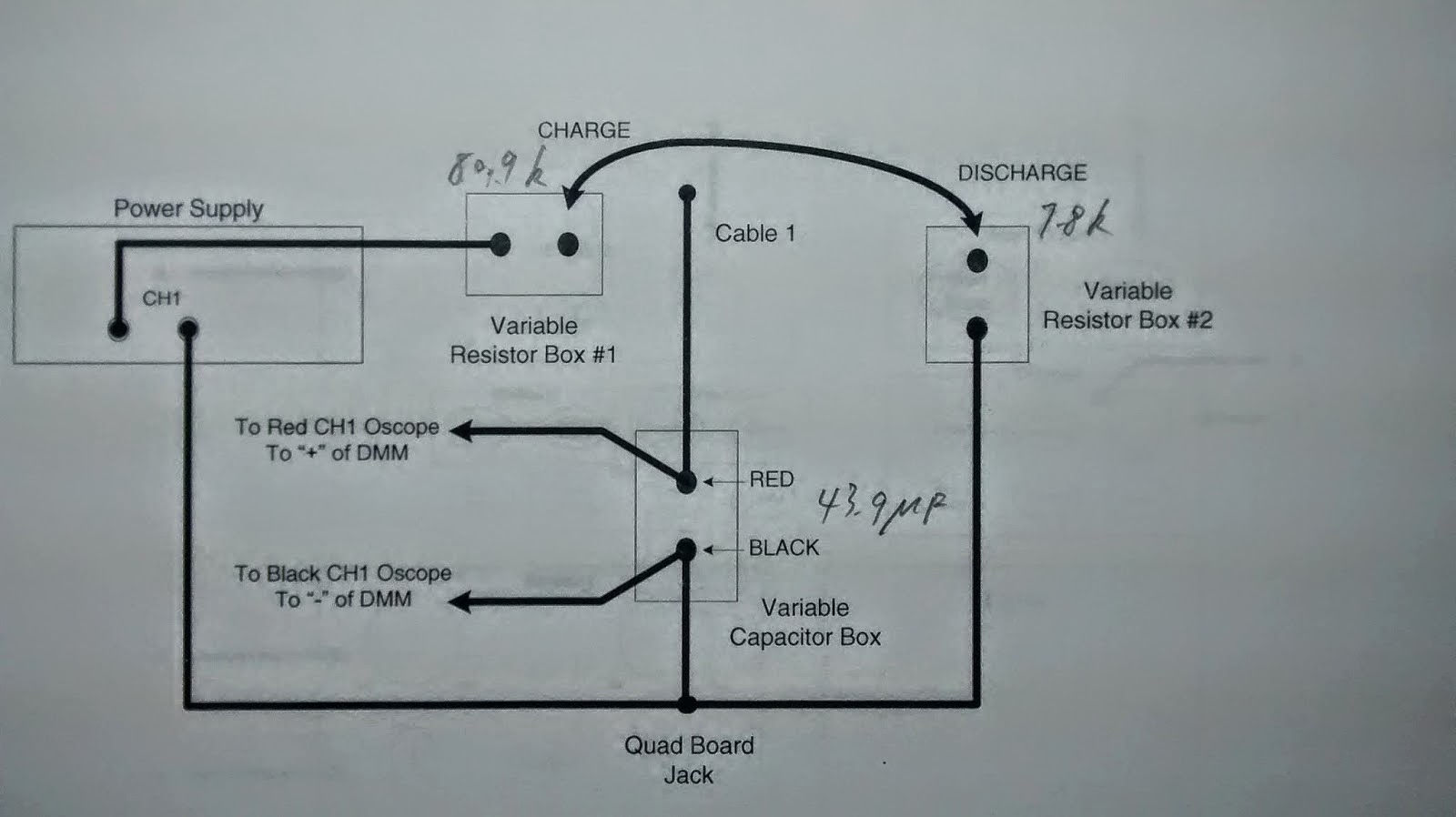
First, we found the values of the components when the circuit is charged and discharged in the circuits below.
We used a stopwatch and a voltmeter to measure the voltage of the charging capacitor within 20 seconds.
Materials 1 Voltmeter and 1 stopwatch (optional), 1 oscilloscope, 2 variable resistors, 1 33 microfarad capacitor, cables.
For a charging time of about 20 seconds the voltage was 11 volts. The discharge time was about 2 sectonds.
Leakage Resistance:
Error calculation:
This was how the discharging graph should have appeared over time.

Conclusion:
The lab demonstrated the rapid discharge rate of a capacitor and the reasonable energy storage that can be achieved with the correct circuitry. The experiment was valid and the leakage resistance was about 10 times the charging resistance. This was the same ratio of the charging to discharging times of the capacitor.
Capacitors are electrical components that store energy in the electric field and can rapidly charge or discharge the energy if needed. In this lab we observed the charging and discharging of a capacitor in the circuit as is dumps it energy.
Procedure:
First, we found the values of the components when the circuit is charged and discharged in the circuits below.
We used this oscilloscope to perform the lab but unfortunately it only gave instantaneous voltage. So we illustrated the response of the capacitor charging and discharging.
We used a stopwatch and a voltmeter to measure the voltage of the charging capacitor within 20 seconds.
Materials 1 Voltmeter and 1 stopwatch (optional), 1 oscilloscope, 2 variable resistors, 1 33 microfarad capacitor, cables.
For a charging time of about 20 seconds the voltage was 11 volts. The discharge time was about 2 sectonds.
Leakage Resistance:
Error calculation:
This was how the discharging graph should have appeared over time.

Conclusion:
The lab demonstrated the rapid discharge rate of a capacitor and the reasonable energy storage that can be achieved with the correct circuitry. The experiment was valid and the leakage resistance was about 10 times the charging resistance. This was the same ratio of the charging to discharging times of the capacitor.
Monday, April 14, 2014
Practical Signal Conditioning
Introduction:
The purpose of this lab was to use an operational amplifier to perform an operation and observe a signal. We used a LM35 semiconductor to translate the ambient air temperature into a voltage signal. This would give us a temperature which would be converted into the Fahrenheit scale from the Celsius scale through the op amp.
Procedure:
We tested the LM35 with 9 V into it relative to ground and seeing what voltage we get as output. We go an output current of 220 mA which was a magnitude representation of the ambient room temperature.
We found the necessary and available resistors to get the proper conversion factors to convert the signal voltage into the comparable Fahrenheit voltage.
 We then connected the LM35 to the op amp into the circuit shown. We also used a potentiometer to adjust the input voltage and the output we got:
We then connected the LM35 to the op amp into the circuit shown. We also used a potentiometer to adjust the input voltage and the output we got:
The purpose of this lab was to use an operational amplifier to perform an operation and observe a signal. We used a LM35 semiconductor to translate the ambient air temperature into a voltage signal. This would give us a temperature which would be converted into the Fahrenheit scale from the Celsius scale through the op amp.
Procedure:
We tested the LM35 with 9 V into it relative to ground and seeing what voltage we get as output. We go an output current of 220 mA which was a magnitude representation of the ambient room temperature.
 |
| Add caption |
 We then connected the LM35 to the op amp into the circuit shown. We also used a potentiometer to adjust the input voltage and the output we got:
We then connected the LM35 to the op amp into the circuit shown. We also used a potentiometer to adjust the input voltage and the output we got:
Using the temperature equation we found the output current to be 0716 A.
The error is shown here.
Conclusion:
This application of op amps demonstrates a practical use of signal conditioning for observing the temperature. It is much more convenient to have a real time temperature with simple signals than to have to convert the temperatures otherwise. The error may have be due to approximations in calculations.
Tuesday, April 1, 2014
Operational Amplifiers 1
Introduction:
The purpose of this lab is to condition a signal from a voltage input to a required voltage output.
- Set up voltage divider circuit in order to obtain signal voltage in DC
- Set up Inverting op amp circuit that conditions signal from 0 to 1 v to 0 to -10v
- measure the values
- conclusion
Procedure:
We first had to find the necessary resistors for this circuit by finding an appropriate ratio and looking at the available resistors.
-The sensor may only output a maximum of 1 mA of current.
Vcc = 12 V.
Vee = -12 V.
Vin = 0 V to +1 V.
Vout = 0 V to -10 V.
Then we created a voltage dividing circuit that would give us the correct 1 V drop across the input and output, which can be modified with the POT.
Ry = 909 Ohm
Rx_min=1152 Ohms, but we will use 1300 ohms as We used a 1300 Ohm resistor to be safe.
For Rx at 1300 Ohms we recalculated
Ry = 118 Ohms
To avoid unappreciable loading of the divider circuit with too low resistances we used a 10k Ohm Rx value instead.
These values are what we used for our model.
By decreasing the value of the POT to a value lower than 909, we were able to obtain necessary voltages for the signal input.
This is what our circuit and testing looked like.
 Testing for all the voltages and caluclating the necessary values gave us the following table.
Testing for all the voltages and caluclating the necessary values gave us the following table.
The purpose of this lab is to condition a signal from a voltage input to a required voltage output.
- Set up voltage divider circuit in order to obtain signal voltage in DC
- Set up Inverting op amp circuit that conditions signal from 0 to 1 v to 0 to -10v
- measure the values
- conclusion
Procedure:
We first had to find the necessary resistors for this circuit by finding an appropriate ratio and looking at the available resistors.
-The sensor may only output a maximum of 1 mA of current.
Vcc = 12 V.
Vee = -12 V.
Vin = 0 V to +1 V.
Vout = 0 V to -10 V.
Then we created a voltage dividing circuit that would give us the correct 1 V drop across the input and output, which can be modified with the POT.
Ry = 909 Ohm
To make sure the resistor Rx does not surpass the power limit we calculated the minimum possible resistance.
For Rx at 1300 Ohms we recalculated
Ry = 118 Ohms
To avoid unappreciable loading of the divider circuit with too low resistances we used a 10k Ohm Rx value instead.
These values are what we used for our model.
By decreasing the value of the POT to a value lower than 909, we were able to obtain necessary voltages for the signal input.
This is what our circuit and testing looked like.
 Testing for all the voltages and caluclating the necessary values gave us the following table.
Testing for all the voltages and caluclating the necessary values gave us the following table.
Conclusion:
The results conclude that there was a gain of -10 through the OP amp, which conditioned the signal to the desired voltage. The current did not exceed 1 milliamp and the voltage divider resistor remained in tact. We were able to successfully condition a signal for the various voltages and see the expected gains.
Thevenin Equivalents
Introduction:




Using the previous two results we found the maximum load resistance that the circuit could hold.
To test the theory of Thevenin equivalence in a practical application we set up a circuit like the one below and made measurements of the load resistance and Thevenin elements.


Conclusion:
In practice the Thevenin equivalent measurements were useful in setting up a loaded circuit and analyzing the output. The theorem only left a small percent error when performed experimentally. It could also further allow us to change the resistance if need be for different goals.
Thevenin equivalents are useful in designing and analyzing variable load elements in a circuit. We can model a system using such analysis and prove that Thevenin equivalence is valid for a practical circuit.
Objective:
The purpose of this lab is to use Thevenin equivalents to analyze a circuit that will carry an unknown load. We would also like to know the voltage that the load must carry and the power lost according to its Thevenin resistance.
Procedure:
In the first part we must determine an open circuit or Thevenin voltage to be used in the circuit shown below.


We found Voc to be 8.64V.
Next we found the voltage Vy in the circuit shown below.


Using the previous two results we found the maximum load resistance that the circuit could hold.
To test the theory of Thevenin equivalence in a practical application we set up a circuit like the one below and made measurements of the load resistance and Thevenin elements.


Conclusion:
In practice the Thevenin equivalent measurements were useful in setting up a loaded circuit and analyzing the output. The theorem only left a small percent error when performed experimentally. It could also further allow us to change the resistance if need be for different goals.
Transistor Switching
Introduction:
The purpose of this lab is to test and measure the effects of transistor switching in a circuit.
Procedure:
In the first part of the lab we set up the circuit below to switch a LED on and off with our fingertip. As long as a voltage can be amplified at the transistor and provide current to the LED it lights up.

.jpeg)
In the next part we used a POT to regulate the voltage at A1 and measured the current at A2. These were our results. The graph of Ic vs Ib gave us the gain (Beta) as the slope of the line being 2.4253.
The purpose of this lab is to test and measure the effects of transistor switching in a circuit.
Procedure:
In the first part of the lab we set up the circuit below to switch a LED on and off with our fingertip. As long as a voltage can be amplified at the transistor and provide current to the LED it lights up.

.jpeg)
In the next part we used a POT to regulate the voltage at A1 and measured the current at A2. These were our results. The graph of Ic vs Ib gave us the gain (Beta) as the slope of the line being 2.4253.
Conclusion:
Transistors make a gain that is related to the ratio of currents in and out of them and allow for rapid switching in the circuit. The transistor did not saturate in our experiment but this model has a listed saturation at 10mA at the collector.
Subscribe to:
Comments (Atom)